Keyword [NetAdapt] [Platform-aware]
Yang T J, Howard A, Chen B, et al. Netadapt: Platform-aware neural network adaptation for mobile applications[C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 285-300.
1. Overview
1.1. Motivation
Existing methods simplify networks based on indirect metrics, such as MACs or weights, instead pf latency and energy consumption.
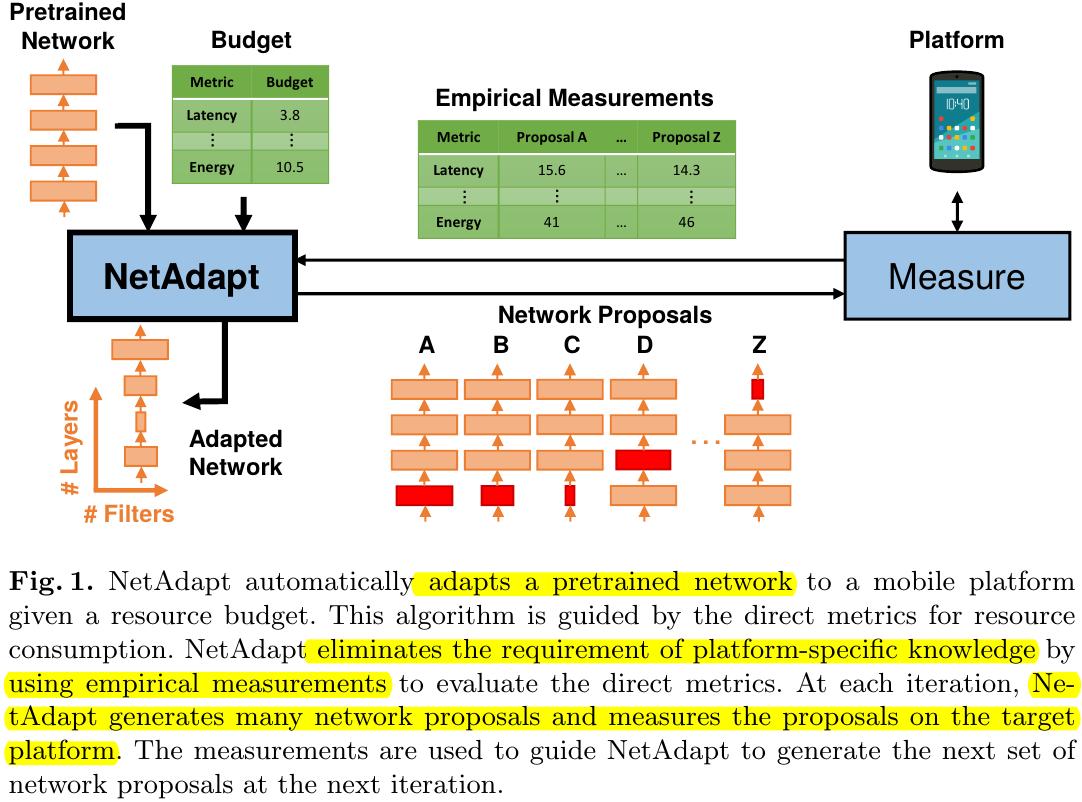
In this paper, it proposes NetAdapt to automatically adapts a pre-trained network to mobile platform given a resource budget.
1) Incorporate direct metrics into algorithm, evaluated using empirical measurements (eliminates the requirement of platform-specific knowledge).
2) Trade-offs on both mobile CPU and mobile GPU.
3) For the K-layer network: Get K network proposals (remove filters from a single Conv or FC)→Choose best proposal→Iteration.
1.2. Metrics
The relationship between an indirect metric and the corresponding direct metric can be highly non-linear and platform-dependent.

1.3. Contribution
1) Framework with direct metrics, empirical measurement (don’t need platform-specific knowledge).
2) Automated constrained network optimization algorithm.
2. Related Works
1) pruning-based methods (energy-aware pruning).
2) Decomposition.
3) Quantization.
3. Algorithm
3.1. Problem Formulation
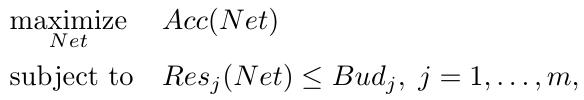
1) $Res_j$. evaluates the direct metric for source consumption of the $j^{th}$ resource.
2) $Bud_j$. the budget of the $j^{th}$ resource
The resource can be latency, energy, memory footprint or a combination of them.
Then break the problem into a series of easier problems, solves it iteratively.
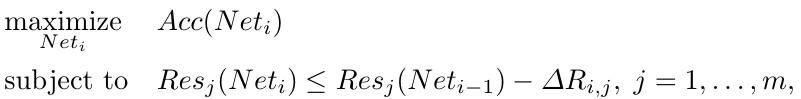
1) $i$. the $i^{th}$ iteration.
2) $Net_0$. initial pre-trained network.
3) $\Delta R_{i,j}$. the constraint tightens for the $j^{th}$ resource in the $i^{th}$ iteration, can vary from iteration to iteration. (Resource Reduction Schedule).
Algorithm terminates when $Res_j (Net_i - 1) - \Delta R_{i,j} \le 0$ for every resource type.
3.2. Details
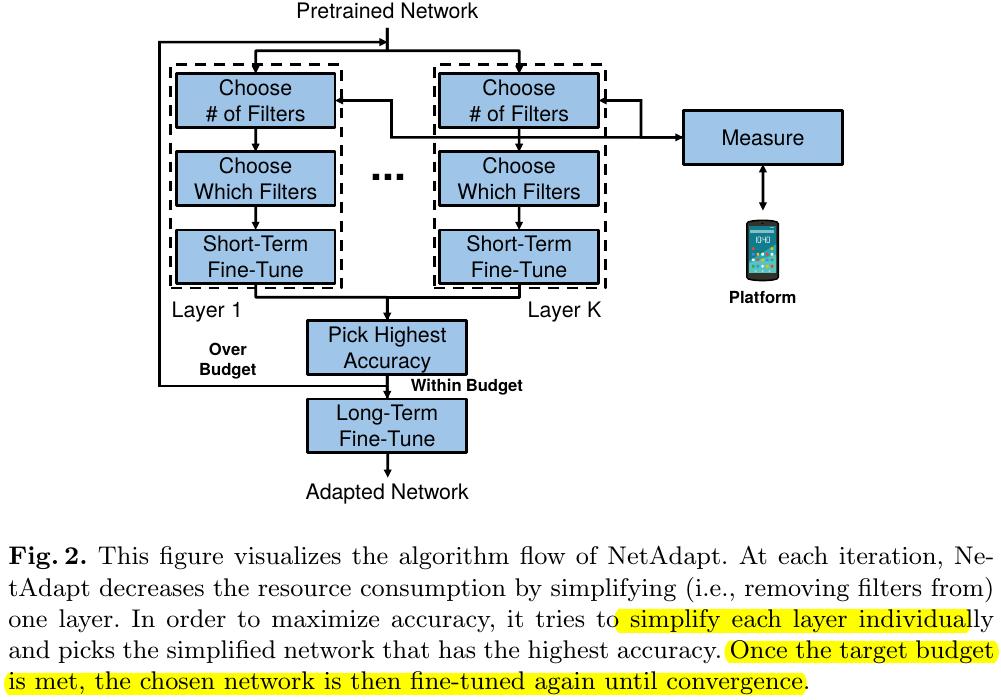

3.2.1. Choose Number of Filters
1) Determine how many filters to preserve in a specific layers based on empirical measurements.
2) The maximum number of filters that can satisfy the current resource constraint will be chosen.
3) When removing operation applys to a layers, the associated layers also need to be change.
3.2.2. Choose Which Filters
1) use magnitude-based method. $N$ filters that have the largest L2-norm magnitude will be kept.
3.2.3 Short-/Long-Term Fine-Tune
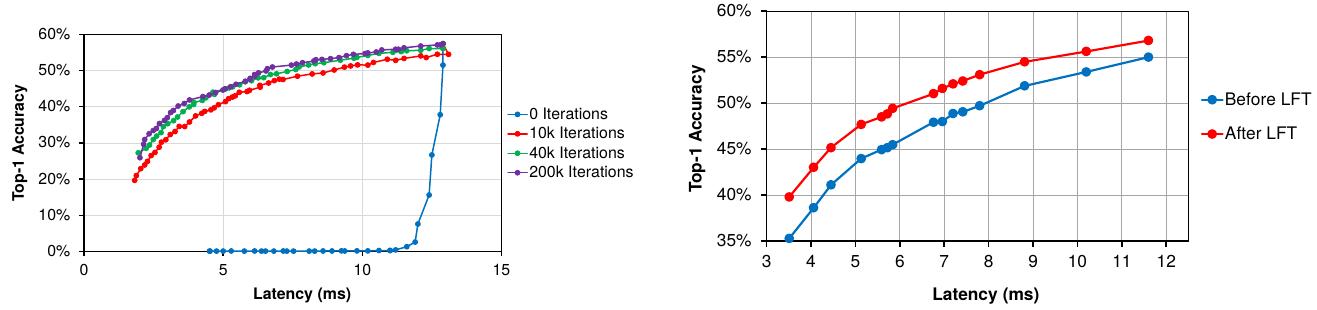
1) Short-term fine-tune has fewer iterations than long-term fine-tune
2) Short-term fine-tune is especially important while adapting small networks with a large resource reduction. Otherwise acc will drop to 0.
3) Fine-tune until qual to acc.
3.3. Fast Resource Consumption Estimation
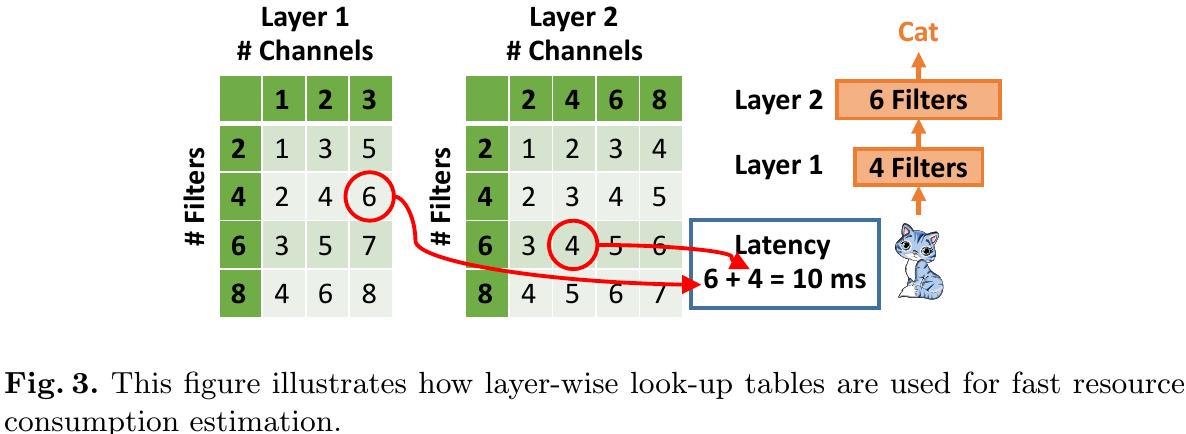
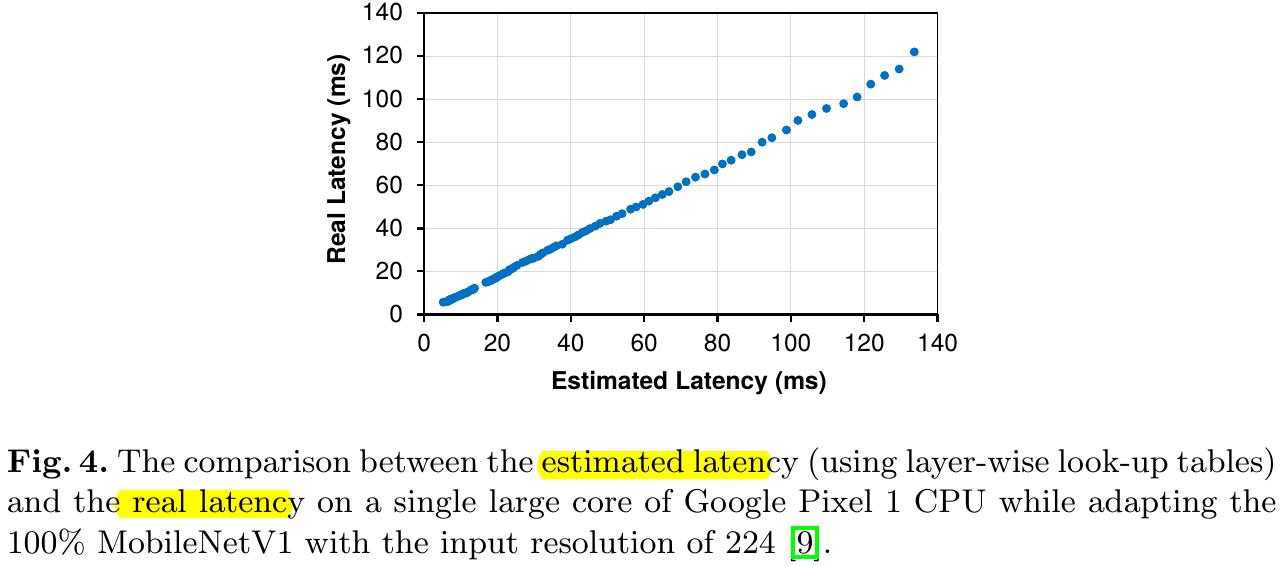
1) Measuring the resource consumption proposal network is slow and hard to parallelize.
2) Solve this problem by building layer-wise look-up tables with pre-measured resource consumption of each layer.
3) The size of network-wise table will grow exponentially with the number of layers.
4. Experiments
4.1. Details for MobileNetv1
1) Adapt each depthwise layer with the corresponding pointwise layers.
2) When adapting the small MobileNetV1, $\Delta R_{i,j}$ starts at 0.5 and decays at the rate of 0.96 per iteration.
3) Training set of ImageNet (long-term fine-tune) is split into New_training Set (short-term fine-tune). and Holdout Set (pick best-acc network) .
4) Long-term fine-tune LR is 0.045. shot-term fine-tune is 0.0045.
4.2. Ablation Study
4.2.1 The Impact of Resource Reduction Schedules

1) Using larger resource reduction at each itertation increases the adaption speed (less adpation iterations)
2) With the same number of total iterations, the results suggests that a smaller initial resource reduction with a slower decay is preferable.
4.3. Architecture Analysis

1) NetAdapt removes more filters in layers 7 to 10, but fewer in layer 6. Since feature size is reduced in layer 6, hypothesize that when the feature size is reduced, more filters are needed to avoid creating an information bottleneck.
2) NetAdapt keeps more filters in layer 13 (last Conv). More features are needed by the last FC to do classification.